OFRG

OFRG, or Oligonucleotide Fingerprinting of rRNA Genes, is a method that allows the identification of arrayed ribosomal RNA genes (rRNA) through a series of hybridization experiments using small DNA probes. A particular important problem is to detect hybridized DNA clusters (called "polonies") in the greyscale image. In PCR experiments, polonies are formed by mixing sample DNA molecules into a gel matrix and then amplified by PCR reagents. Thus, polonies grow slowly outward and are centered at the randomly-placed DNA molecule from which they originated.

The following figure shows an example of polony images in our experiments. These black dots are hybridized DNA clusters, and are randomly distributed and sometimes overlapping with each other.

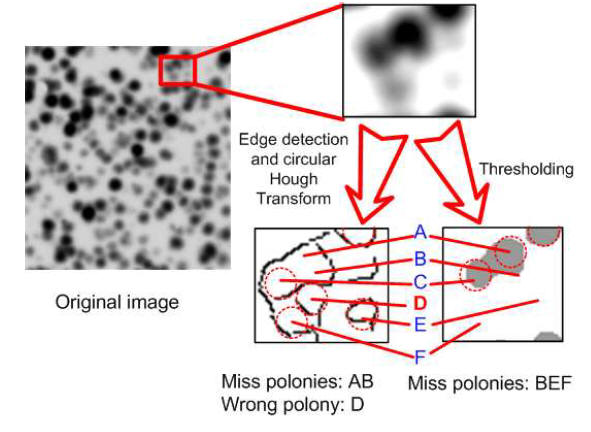
A paper which is focus on identifying these polonies (especially overlapping polonies) has been published on the 10th IEEE International Conference on Bioinformatics and Bioengineering (BIBE 2010). You can download the paper here.

Traditional Chinese Medicine

Traditional Chinese Medicine (TCM) has a history of thousands of years, and is an active research focus of pharmacology, clinical medicine and other areas in China. As a research assistant of a state-funded project, I helped pharmacologists develop new anti-inflammatory drugs from a traditional Chinese Medicine recipe. By extracting key features from a drug's 2-dimensional chemical structures, I used several machine learning algorithms to predict the activity of inhibitors on Cyclooxygenase II (COX2), a key enzyme in human inflammatory pathway. Two research papers have been published on the project.

The project studies Cinnamomi Ramulus Decoction(or CRD, "桂枝汤"), a widely used traditional Chinese compound. CRD is a very famous traditional Chinese medicine compound, and is the principle compound listed in "Shanghan Lun" (Treatise on Cold Pathogenic Diseases, "伤寒论(张仲景)"). This is a very useful anti-fever and anti-inflammation drug. Chemical and pharmacological analysis shows that enzymes of cyclooxygenase (COX) isoformates (COX-1 and COX-2), and secretion of prostaglandin E2 (PGE-2), play a key role during the inflammation process of human body.

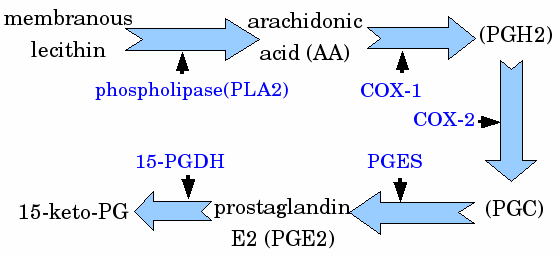Pathway of human inflammation

Researchers have found that many COX-2 inhibitors share a common structure, and in this project, we are using Quantitative Structure-Activity Relationship (QSAR) technique to predict the activities of these inhibitors.

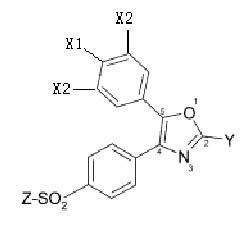Common structures of COX-2 inhibitors

Machine learning algorithms are used to predict the activity of these inhibitors. Several structural and biological properties, like hydrophobic parameter (CLOGP), constant of molecular refraction (CMR), length of substitution, quantum-chemical descriptors, graph and topological indices, etc, are extracted from computer simulations. And then, we build several machine learning models like support vector machines, boosting, genetic algorithm, etc.

Soccer Robots

The project aims at the robot self-localization problem: how can a soccer robot identify its position quickly and precisely during the match? This is crucial for a soccer robot to play and win in a match (imagine in a human world, what if a soccer player doesn't know where he is?). Also this problem has a wide application, for example, explore unknown territory for a robot under the sea or on the moon.

This project is also a part of the SRT (Student Research Training project) in Tsinghua University. So I was also a teaching assistant and was in charge of a robotic class where 40 undergraduate students enrolled to develop software programs for soccer robots.

How it works?

The robot in our project is actually a three-wheel battery-driven vehicle, with two webcams on its head (see the image on the right). This is a mini LINUX-based robot operating system, and you can write C++ programs to control the camera, the motor, and to communicate with other soccers via wireless network. Robots find their locations based on two kinds of information, commands sent to the motor (like, "turn right 45 degree" or "go straight for 2 meters", etc) and images captured from its camera.

It seems complicated to process the visual information from the camera, but in the soccer match, there is something crucial for identification: the position of the goals and the appearance of the white lines in the football field.

I found MCMC (Monte-Carlo Markov Chain) is a suitable algorithm to do this. This is an iterative algorithm, each round takes motor commands and camera images as input. When images are captured, the algorithm looks for goals (by the color of the goals) and side lines (using Canny edge detection and Hough Transform). This is the "true" scene that a robot is seeing.

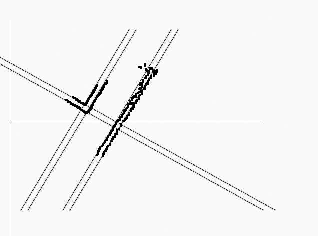White sidelines in camera	Edge detection	Hough transform

Then, the algorithm uses a sampling algorithm (Monte-Carlo) to sample all possible positions in the football field. For each position, the robot tries to answer the following question: what the goal and the side line should look like, if I were in this position? Then, it compares this "predicted" scene with the true scene. If both match, it is more likely that the robot is really at the assumed position.

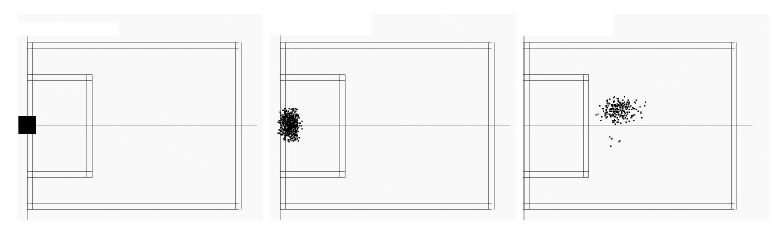Particle distribution with known initial position. 0 move (left), 1 move (middle) and 17 moves (right).

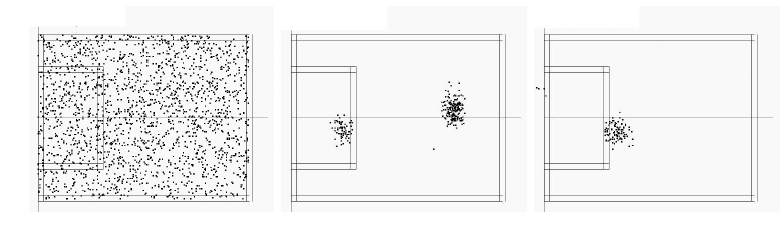Particle distribution with unknown initial position. 0 move (left), 1 move (middle) and 6 moves (right).