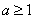 and
and
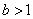 be constants, let
be constants, let
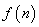 be a function, and let
be a function, and let
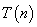 be defined on the nonnegative integers by the recurrence:
be defined on the nonnegative integers by the recurrence:Master Method
| Back to cs141 |
Compared with the iteration method, the master method is much easier to use once you understand how to use it. The hardest part about the master method is understanding the language of the master theorem.
Let
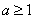 and
and
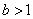 be constants, let
be constants, let
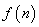 be a function, and let
be a function, and let
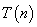 be defined on the nonnegative integers by the recurrence:
be defined on the nonnegative integers by the recurrence:
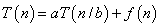
where we interpret
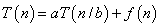 to mean either
to mean either
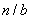 or
or
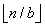 . Then
. Then
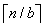 can be bounded asymptotically as follows:
can be bounded asymptotically as follows:
1. If
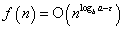 for some constant
for some constant
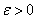 , then
, then
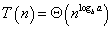 .
.
2. If
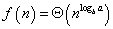 , then
, then
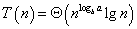 .
.
3. If
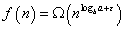 for some constant
for some constant
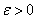 , and if
, and if
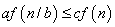 for some constant
for some constant
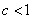 and all sufficiently large
and all sufficiently large
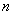 , then
, then
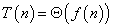 .
.
Basically all you have to do to solve a recurrence relation is figure out which of the three cases your recurrence falls into and apply the given formula to get the answer!
|
Practice Problems |