SIGCSE 2006 DC Application

Titus Winters (titus@cs.ucr.edu)

Department Computer Science & Engineering Engineering Building Unit II Room 465
University of California at Riverside, 92521
Phone: 909 262 0385
Keywords: accreditation, data mining, curriculum assessment
Personal Homepage: http://www.cs.ucr.edu/~titus
Advisor: Tom Payne (thp at cs ucr edu)

Topic Grouping of Questions for Assessment

Introduction

Instigated by the recent press for "continuous improvement processes" in education [1], our project seeks to build a system capable of numerically quantifying the level of coverage and student understanding for the various topics that make up each course in our curriculum [7]. Our ultimate goal for the project is to answer questions like: It was decided early on in this project that we would focus on making only minimal changes to existing teaching methods. In particular, we have developed grading tools that record scores for each student for each question, rather than only aggregated scores for each student on a each instrument. Deployment of these tools have been generally successful, providing us with a rich data source of per-question scores.

Topic Extraction

The key to answering many or all of our goal questions is being able to label questions by topic. Having instructors manually identify the topic for every question asked in a semester was judged as too onerous, so we rely on finding automated methods for topic extraction. Our goal is to produce groups of questions that are viewed as testing the same topic. By examining one or two samples from those groups, instructors can quickly label the group. This reduces the instructor workload from one input per question to one input per topic. Once questions are labeled with topic, the goal questions become simple averages of the appropriate subsets of the data.

The focus of this work is therefore to find algorithms from data mining which produce question groupings similar to those that would be produced by humans. Note that this is not necessarily the same as finding the "common factors" using educational statistics techniques like CFA ([6]): we are not looking for unknown factors, we are looking to match against known factors (topics.)
Evaluation
To evaluate each algorithm we are examining, it is necessary to have an already-known "correct answer" for each data set. For each class dataset we are evaluating, we have asked the instructor for that class to produce groupings of questions that they would regard as correct. (The instructors are given the text of the question to evaluate this.) They may produce as many or as few groups as they like, each question may occur in any number of groups: none if there are no questions like it, or more than one group if it corresponds to multiple topics.

Given these groups, we extract all pairs of questions that are valid to be paired together. For each algorithm that we evaluate, we determine group membership according to that algorithm, and again create the pairs of questions that are grouped together. The validity of the algorithm is then measured by determining the overlap between these two sets of pairs: the "correct" answer, and the generated answer. Additionally, many algorithms give a "certainty" to each question. By varying our certainty, we get a parametric plot of accuracy.

To visualize the correctness of each algorithm, we generate Precision vs. Recall graphs. As we vary the certainty parameter, starting with only the questions that are most certain, we get larger and larger groups of question pairings. For each setting of the certainty parameter, we evaluate the precision and the recall of the produced pairing sets. Precision is the percentage of pairs produced by the algorithm that is present in the correct answer. Recall is the percentage of pairings in the correct answer that is produced by the algorithm. Any algorithm can achieve perfect recall by putting all questions into the same group, but this results in poor precision. Alternatively, an algorithm that only reports one group with two correctly-paired questions in it achieves perfect precision, but poor recall. To maximize precision and recall simultaneously, the algorithm must produce exactly the same groups that the humans produced.

Generating Data

Over the past year we have evaluated more than a dozen candidate algorithms (notably [2-6]) to determine their suitability for this task. Remarkably, most algorithms perform worse than random chance on this task. That is, if groupings were made completely at random, the resulting precision would be greater than the groupings produced by the candidate algorithms. This indicates that the algorithms are finding some structure to the data, but it is not structure that corresponds well with the human notion of "topic."

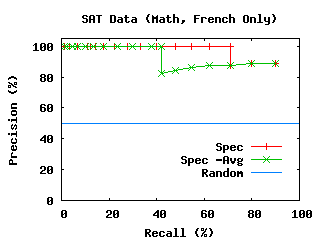With the assumption that the flaw was in the lack of topic structure in the data, rather than an inability for numerous published algorithms to perform, we gathered score data from many people on questions with known topics. We used two 40-question quizzes, one drawn from Trivial Pursuit questions, and one drawn from questions out of SAT Subject Test study guides. Both quizzes had 4 topics with 10 questions each. The Trivial Pursuit tested Science and Nature, Sports and Leisure, Arts and Entertainment, and Geography. The SAT tested Math, Biology, World History, and French. Both were organized as short-answer tests, where the correct answers were two words or less. A string-matching algorithm was used to compare given answers against the list of known good answers to discount misspellings as a source of error, and all of the "incorrect" answers were checked by hand to ensure that they were in fact incorrect. Over a period of about a week these quizzes were available online. The Trivia quiz was completed by 467 participants, the Academic quiz was completed by 297.

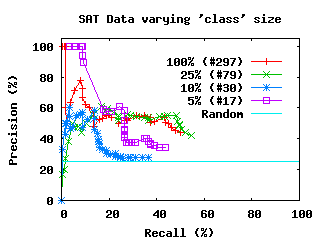
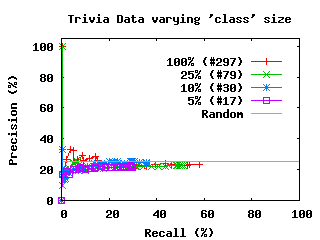The results are fairly conclusive. The Academic data clearly confirms that some topics present a deeper knowledge and level of understanding, while others are more based on isolated bits of knowledge. The Math and French questions from the Academic quiz can be easily separated by most of our algorithms, with accuracy greater than 85%. Even when the number of "students" in the dataset is reduced to normal class sizes of 20 to 30, there is sufficient structure in the Math and French data to separate out these two subjects. In the whole four-topic data, there is more noise, but the results are still significantly better than random chance. Depending on the algorithm utilized for the grouping, precision remains in the 50-60% range.

In contrast, the data from the Trivia test behaves poorly. Success in answering trivia questions does not require deep knowledge of the topic, but isolated fact retrieval. The trivia data, even with nearly 500 "students" in the dataset, is effectively inseparable, producing results that are no better than random chance with most algorithms. On the trivia data, most candidate algorithms produce worse-than-random results similar to the original class data.

Open Issues

The question that is raised by this work is concerning: Why does actual class data behave like the trivia data? There are a number of hypotheses for answering this question, including: With the exception of the final (unlikely) hypothesis, any of the above are interesting outcomes. This experiment unfortunately appears to confirm that the goal of a score-based algorithm for grouping questions by topic is fundamentally infeasable.

Current Stage in my Program of Study

I am scheduled to defend my dissertation in the Spring of 2006.

What I Hope to Gain from participating in the Doctoral Consortium

I have attended the DC for the past two years. In both of those cases I have come out of the day with a much stronger grasp of both the work ahead of me as well as the importance of my work and relation between what I am doing and the rest of the community. Working primarily in isolation here at UCR, the DC is my major opportunity for seeing firsthand what other doctoral students in the area are doing, as well as networking with experts in the field. The Doctoral Consortium is in many ways the highlight of my academic year. This year it will come at the perfect time to adjust the focus and emphasis of my dissertation results. As such, I am highly anxious to participate again, one last time as a student.

Bibliographic References

  1. ABET - Accreditation Board for Engineering and Technology
  2. Barnes, T. The Q-Matrix Method of Fault Tolerant Teaching in Knowledge Assessment and Data Mining. PhD Thesis, North Carolina State University. 2003.
  3. Gentle, J. E. "Singular Value Factorization." 3.2.7 in Numerical Linear Algebra for Applications in Statistics. Berlin: Springer-Verlag, pp 102-103, 1998.
  4. Lee, D., Seung H. S. Algorithm for Non-Negative Matrix Factorization. In proceedings, Advances of Neural Processing Systems v. 13, 2001.
  5. Ng, A., Jordan, M. On Spectral Clustering: Analysis and an Algorithm. In proceedings, Advances of Neural Processing Systems v. 13, 2001.
  6. Spearman, C. General Intelligence, Objectively Determined and Measured. American Journal of Psychology, v. 15. pp 201-293. 1904.
  7. Winters, T., Payne, T. What Do Students Know? In proceedings, First International Computing Education Research Workshop (ICER05).