Suppose we have the following recurrence relation:
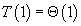
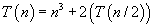
then:
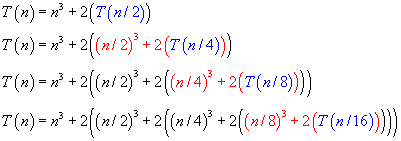
Each iteration, the recurrence is replaced with its value as established by the original recurrence relation. Notice that each iteration the
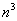 term is replaced with
term is replaced with
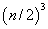 , then
, then
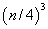 , and so on. Now that we've done a few iterations, let's simplify and see if there is a recognizable pattern.
, and so on. Now that we've done a few iterations, let's simplify and see if there is a recognizable pattern.
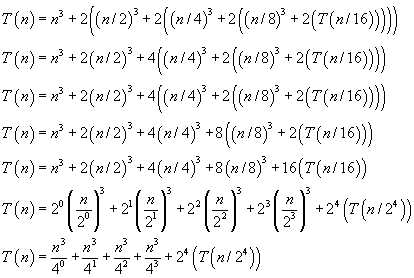
There's a definite pattern in all but the last term of the equation, and the last term seems to be related by the power that 2 is raised to. Now the question is: When is this going to stop?
From the original problem we know that:
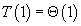 . We can say that:
. We can say that:
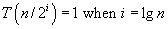
Now we can write our simplified equation in terms of
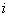 .
.
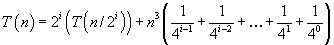
Now since
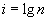 ,
,
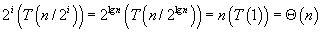 . We can also recognize the second half of the equation as a geometric series; allowing us to re-write the equation as:
. We can also recognize the second half of the equation as a geometric series; allowing us to re-write the equation as:
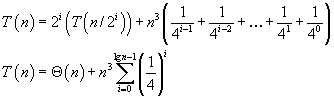
Although we could work out the summation, it's much easier to realize that this is a finite geometric series, meaning that the summation will be a constant. Since any constant is
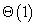 , we are left with:
, we are left with:
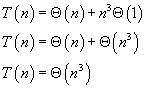
So, the time complexity of this recurrence relations is
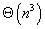 .
.
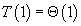
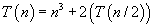
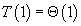
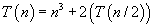
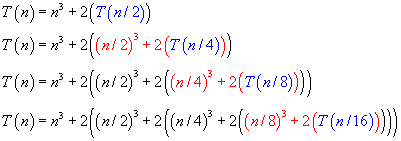
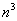 term is replaced with
term is replaced with
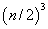 , then
, then
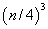 , and so on. Now that we've done a few iterations, let's simplify and see if there is a recognizable pattern.
, and so on. Now that we've done a few iterations, let's simplify and see if there is a recognizable pattern.
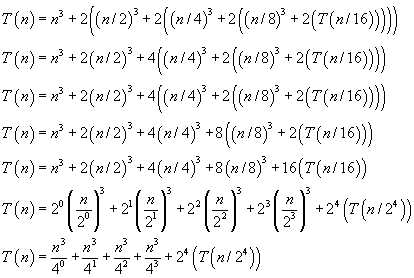
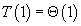 . We can say that:
. We can say that:
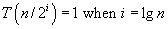
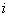 .
.
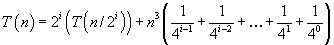
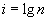 ,
,
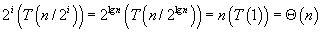 . We can also recognize the second half of the equation as a geometric series; allowing us to re-write the equation as:
. We can also recognize the second half of the equation as a geometric series; allowing us to re-write the equation as:
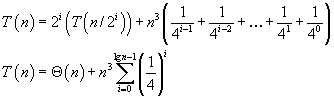
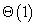 , we are left with:
, we are left with:
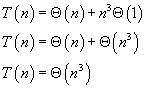
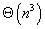 .
.